题1

2395. 和相等的子数组

难度简单

给你一个下标从 0 开始的整数数组 nums ，判断是否存在两个长度为 2 的子数组且它们的和相等。注意，这两个子数组起始位置的下标必须 不相同 。

如果这样的子数组存在，请返回 true，否则返回 false 。

子数组 是一个数组中一段连续非空的元素组成的序列。

示例 1：
输入：nums = [4,2,4]
输出：true
解释：元素为 [4,2] 和 [2,4] 的子数组有相同的和 6 。
示例 2：
输入：nums = [1,2,3,4,5]
输出：false
解释：没有长度为 2 的两个子数组和相等。
示例 3：
输入：nums = [0,0,0]
输出：true
解释：子数组 [nums[0],nums[1]] 和 [nums[1],nums[2]] 的和相等，都为 0 。
注意即使子数组的元素相同，这两个子数组也视为不相同的子数组，因为它们在原数组中的起始位置不同。
提示：

2 <= nums.length <= 1000

-109 <= nums[i] <= 109

析

两数相加，将和放入Hash表中，若计算出来的和已经在Hash表中存在，则返回true；若直到最后都没有找出来，返回false。

解

func findSubarrays(nums []int) bool {
    m := make(map[int]struct{})

    for i := 1; i < len(nums); i++ {
        v := nums[i] + nums[i-1]
        if _, ok := m[v]; ok {
            return true
        }
        m[v] = struct{}{}
    }
    return false
}

题2

2396. 严格回文的数字

难度中等

如果一个整数 n 在 b 进制下（b 为 2 到 n - 2 之间的所有整数）对应的字符串全部都是 回文的 ，那么我们称这个数 n 是 严格回文 的。

给你一个整数 n ，如果 n 是 严格回文 的，请返回 true ，否则返回 false 。

如果一个字符串从前往后读和从后往前读完全相同，那么这个字符串是 回文的 。

示例 1：
输入：n = 9
输出：false
解释：在 2 进制下：9 = 1001 ，是回文的。
在 3 进制下：9 = 100 ，不是回文的。
所以，9 不是严格回文数字，我们返回 false 。
注意在 4, 5, 6 和 7 进制下，n = 9 都不是回文的。
示例 2：
输入：n = 4
输出：false
解释：我们只考虑 2 进制：4 = 100 ，不是回文的。
所以我们返回 false 。
提示：

4 <= n <= 105

析

进制的范围是[2, n-2]，考虑n-2进制的情况，表示为n/(n-2) « 1 | n%(n-2) = 12，必定不是回文，因此直接返回false。

解

func isStrictlyPalindromic(n int) bool {
    return false
}

题3

2397. 被列覆盖的最多行数

难度中等

给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ，表示你需要选出的列数。

如果一行中，所有的 1 都被你选中的列所覆盖，那么我们称这一行 被覆盖 了。

请你返回在选择 cols 列的情况下，被覆盖 的行数最大为多少。

示例 1：
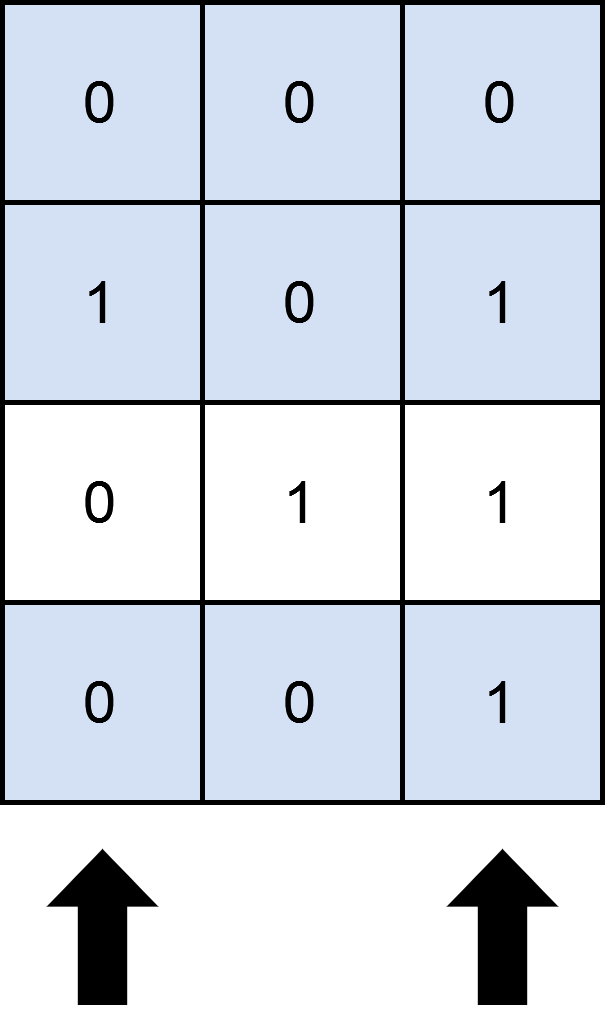
输入：mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
输出：3
解释：
如上图所示，覆盖 3 行的一种可行办法是选择第 0 和第 2 列。
可以看出，不存在大于 3 行被覆盖的方案，所以我们返回 3 。
示例 2：
输入：mat = [[1],[0]], cols = 1
输出：2
解释：
选择唯一的一列，两行都被覆盖了，原因是整个矩阵都被覆盖了。
所以我们返回 2 。
提示：

m == mat.length

n == mat[i].length

1 <= m, n <= 12

mat[i][j] 要么是 0 要么是 1 。

1 <= cols <= n

析

可dfs爆搜（比赛时是这么做的）
由于矩阵中的值只包含0、1，可使用位运算，先计算出矩阵每行用二进制表示的数，然后枚举所有[0, 1<<n]范围内二进制表示中1个数为cols的数字state，通过&按位与操作计算state可以覆盖的行数，最后取最大值即可。参考题解

解

// 统计二进制表示下数字中1的个数
func countOne(num int) (ans int) {
    for num > 0 {
        num &= num-1
        ans++
    }
    return ans
}

func maximumRows(matrix [][]int, numSelect int) int {
    m := len(matrix)
    n := len(matrix[0])
    mt := make([]int, m)
    // 将矩阵的每一行转换成二进制表示的数字
    for i := range matrix {
        for j, v := range matrix[i] {
            mt[i] |= v << j
        }
    }

    ans := 0

    // 枚举所有[0,1<<n]区间内1个数为numSelect个的数字
    for state := 0; state < 1<<n; state++ {
        if countOne(state) != numSelect {
            continue
        }

        // 统计当前选择可以覆盖的行数
        // 若state&row==row则表示row为state的子集，row可以被state完全覆盖
        cnt := 0
        for _, row := range mt {
            if state & row == row {
                cnt++
            }
        }
        if cnt > ans {
            ans = cnt
        }
    }
    return ans
}

题4

2398. 预算内的最多机器人数目

难度困难

你有 n 个机器人，给你两个下标从 0 开始的整数数组 chargeTimes 和 runningCosts ，两者长度都为 n 。第 i 个机器人充电时间为 chargeTimes[i] 单位时间，花费 runningCosts[i] 单位时间运行。再给你一个整数 budget 。

运行 k 个机器人 总开销 是 max(chargeTimes) + k * sum(runningCosts) ，其中 max(chargeTimes) 是这 k 个机器人中最大充电时间，sum(runningCosts) 是这 k 个机器人的运行时间之和。

请你返回在 不超过 budget 的前提下，你最多可以连续运行的机器人数目为多少。

示例 1：
输入：chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25
输出：3
解释：
可以在 budget 以内运行所有单个机器人或者连续运行 2 个机器人。
选择前 3 个机器人，可以得到答案最大值 3 。总开销是 max(3,6,1) + 3 * sum(2,1,3) = 6 + 3 * 6 = 24 ，小于 25 。
可以看出无法在 budget 以内连续运行超过 3 个机器人，所以我们返回 3 。
示例 2：
输入：chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19
输出：0
解释：即使运行任何一个单个机器人，还是会超出 budget，所以我们返回 0 。
提示：

chargeTimes.length == runningCosts.length == n

1 <= n <= 5 * 104

1 <= chargeTimes[i], runningCosts[i] <= 105

1 <= budget <= 1015

析

与239. 滑动窗口最大值思路相似。利用滑动窗口与单调栈（或大顶堆）维护窗口内最大值，同时根据题意max(chargeTimes) + k * sum(runningCosts) < budget维护滑动窗口大小，记录最大窗口值即可。

解

func maximumRobots(chargeTimes []int, runningCosts []int, budget int64) int {
    // 单调队列
    s := make([]int, 0)
    i, j := 0, 0
    n := len(chargeTimes)
    var sum int64 = 0
    ans := 0
    for ; j < n; j++ {
        // 及时弹出单调队列右侧
        for len(s) > 0 && chargeTimes[s[len(s)-1]] < chargeTimes[j] {
            s = s[:len(s)-1]
        }
        // 入队列
        s = append(s, j)
        sum += int64(runningCosts[j])
        // 滑动窗口条件判断
        for i <= j && int64(chargeTimes[s[0]]) + int64(j-i+1) * sum > budget {
            if s[0] == i {
                s = s[1:]
            }
            sum -= int64(runningCosts[i])
            i++
        }

        if j - i + 1 > ans {
            ans = j - i + 1
        }
    }
    return ans
}

最后修改于 2022-09-07