题1
2389. 和有限的最长子序列
难度 简单
给你一个长度为
n的整数数组nums,和一个长度为m的整数数组queries。返回一个长度为
m的数组answer,其中answer[i]是nums中 元素之和小于等于queries[i]的 子序列 的 最大 长度 。子序列 是由一个数组删除某些元素(也可以不删除)但不改变剩余元素顺序得到的一个数组。
示例 1:
输入:nums = [4,5,2,1], queries = [3,10,21] 输出:[2,3,4] 解释:queries 对应的 answer 如下: - 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ,所以 answer[0] = 2 。 - 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ,所以 answer[1] = 3 。 - 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ,所以 answer[2] = 4 。示例 2:
输入:nums = [2,3,4,5], queries = [1] 输出:[0] 解释:空子序列是唯一一个满足元素和小于或等于 1 的子序列,所以 answer[0] = 0 。提示:
n == nums.lengthm == queries.length1 <= n, m <= 10001 <= nums[i], queries[i] <= 106
析
- 虽然题目要求子序列(子序列顺序要和原数组保持一致),但是需要拿子序列的和与
queries[i]比较。这里子序列的和并不care子序列的顺序,因此可以使用贪心的思想,将原数组排序,然后从小到大求和直到小于等于queries[i],即可得到答案序列。 - 暴力枚举的时间复杂度为O(n2),可以通过前缀和及二分查找,将时间复杂度降低至O(nlogn)。
解
func bisectRight(nums []int, target int) int {
l, r := 0, len(nums)
for l < r {
m := l + (r-l)>>1
if nums[m] <= target {
l = m + 1
} else {
r = m
}
}
return l
}
func answerQueries(nums []int, queries []int) []int {
sort.Ints(nums)
// 前缀和
presum := make([]int, len(nums)+1)
for i := 1; i < len(presum); i++ {
presum[i] = presum[i-1] + nums[i-1]
}
ans := make([]int, len(queries))
for i, q := range queries {
// 寻找右边界,保证区间长度最大
ans[i] = bisectRight(presum, q) - 1
}
return ans
}
题2
2390. 从字符串中移除星号
难度 中等
给你一个包含若干星号
*的字符串s。在一步操作中,你可以:
- 选中
s中的一个星号。- 移除星号 左侧 最近的那个 非星号 字符,并移除该星号自身。
返回移除 所有 星号之后的字符串**。**
注意:
- 生成的输入保证总是可以执行题面中描述的操作。
- 可以证明结果字符串是唯一的。
示例 1:
输入:s = "leet**cod*e" 输出:"lecoe" 解释:从左到右执行移除操作: - 距离第 1 个星号最近的字符是 "leet**cod*e" 中的 't' ,s 变为 "lee*cod*e" 。 - 距离第 2 个星号最近的字符是 "lee*cod*e" 中的 'e' ,s 变为 "lecod*e" 。 - 距离第 3 个星号最近的字符是 "lecod*e" 中的 'd' ,s 变为 "lecoe" 。 不存在其他星号,返回 "lecoe" 。示例 2:
输入:s = "erase*****" 输出:"" 解释:整个字符串都会被移除,所以返回空字符串。提示:
1 <= s.length <= 105s由小写英文字母和星号*组成s可以执行上述操作
析
- 由题意可得,遇到一个
*需要删除前面一个非*字符,使用栈可以很好得解决这个问题。
解
func removeStars(s string) string {
st := make([]byte, 0)
for i := range s {
if s[i] == '*' {
// 遇到*弹出
st = st[:len(st)-1]
} else {
st = append(st, s[i])
}
}
return string(st)
}
题3
2391. 收集垃圾的最少总时间
难度 中等
给你一个下标从 0 开始的字符串数组
garbage,其中garbage[i]表示第i个房子的垃圾集合。garbage[i]只包含字符'M','P'和'G',但可能包含多个相同字符,每个字符分别表示一单位的金属、纸和玻璃。垃圾车收拾 一 单位的任何一种垃圾都需要花费1分钟。同时给你一个下标从 0 开始的整数数组
travel,其中travel[i]是垃圾车从房子i行驶到房子i + 1需要的分钟数。城市里总共有三辆垃圾车,分别收拾三种垃圾。每辆垃圾车都从房子
0出发,按顺序 到达每一栋房子。但它们 不是必须 到达所有的房子。任何时刻只有 一辆 垃圾车处在使用状态。当一辆垃圾车在行驶或者收拾垃圾的时候,另外两辆车 不能 做任何事情。
请你返回收拾完所有垃圾需要花费的 最少 总分钟数。
示例 1:
输入:garbage = ["G","P","GP","GG"], travel = [2,4,3] 输出:21 解释: 收拾纸的垃圾车: 1. 从房子 0 行驶到房子 1 2. 收拾房子 1 的纸垃圾 3. 从房子 1 行驶到房子 2 4. 收拾房子 2 的纸垃圾 收拾纸的垃圾车总共花费 8 分钟收拾完所有的纸垃圾。 收拾玻璃的垃圾车: 1. 收拾房子 0 的玻璃垃圾 2. 从房子 0 行驶到房子 1 3. 从房子 1 行驶到房子 2 4. 收拾房子 2 的玻璃垃圾 5. 从房子 2 行驶到房子 3 6. 收拾房子 3 的玻璃垃圾 收拾玻璃的垃圾车总共花费 13 分钟收拾完所有的玻璃垃圾。 由于没有金属垃圾,收拾金属的垃圾车不需要花费任何时间。 所以总共花费 8 + 13 = 21 分钟收拾完所有垃圾。示例 2:
输入:garbage = ["MMM","PGM","GP"], travel = [3,10] 输出:37 解释: 收拾金属的垃圾车花费 7 分钟收拾完所有的金属垃圾。 收拾纸的垃圾车花费 15 分钟收拾完所有的纸垃圾。 收拾玻璃的垃圾车花费 15 分钟收拾完所有的玻璃垃圾。 总共花费 7 + 15 + 15 = 37 分钟收拾完所有的垃圾。提示:
2 <= garbage.length <= 105garbage[i]只包含字母'M','P'和'G'。1 <= garbage[i].length <= 10travel.length == garbage.length - 11 <= travel[i] <= 100
析
- 每一个单元(字符)都需要消耗一分钟,可以直接加起来。
- 剩下就是求一辆车需要到达的最远房子,遍历
garbage时使用一个数组维护最右点下标即可。
解
func garbageCollection(garbage []string, travel []int) int {
ans := 0
right := make([]int, 3)
for i, g := range garbage {
// 加上字符长度,即表示收拾这所房子中的所有垃圾所需要的时间
ans += len(g)
for j, v := range "GMP" {
// 更新最右点下标
if strings.Contains(g, string(v)) {
right[j] = i
}
}
}
// 计算3辆车到达最右点需要的时间
for _, r := range right {
for _, v := range travel[:r] {
ans += v
}
}
return ans
}
题4
2392. 给定条件下构造矩阵
难度 困难
给你一个 正 整数
k,同时给你:
- 一个大小为
n的二维整数数组rowConditions,其中rowConditions[i] = [abovei, belowi]和- 一个大小为
m的二维整数数组colConditions,其中colConditions[i] = [lefti, righti]。两个数组里的整数都是
1到k之间的数字。你需要构造一个
k x k的矩阵,1到k每个数字需要 恰好出现一次 。剩余的数字都是0。矩阵还需要满足以下条件:
- 对于所有
0到n - 1之间的下标i,数字abovei所在的 行 必须在数字belowi所在行的上面。- 对于所有
0到m - 1之间的下标i,数字lefti所在的 列 必须在数字righti所在列的左边。返回满足上述要求的 任意 矩阵。如果不存在答案,返回一个空的矩阵。
示例 1:
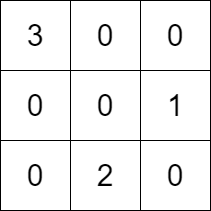
输入:k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] 输出:[[3,0,0],[0,0,1],[0,2,0]] 解释:上图为一个符合所有条件的矩阵。 行要求如下: - 数字 1 在第 1 行,数字 2 在第 2 行,1 在 2 的上面。 - 数字 3 在第 0 行,数字 2 在第 2 行,3 在 2 的上面。 列要求如下: - 数字 2 在第 1 列,数字 1 在第 2 列,2 在 1 的左边。 - 数字 3 在第 0 列,数字 2 在第 1 列,3 在 2 的左边。 注意,可能有多种正确的答案。示例 2:
输入:k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]] 输出:[] 解释:由前两个条件可以得到 3 在 1 的下面,但第三个条件是 3 在 1 的上面。 没有符合条件的矩阵存在,所以我们返回空矩阵。提示:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti
析
- 要确定数字在row、col的先后顺序,可使用拓扑排序实现
- 当出现环时返回空数组
解
func topoSort(edges [][]int, k int) []int {
inDeg := make([]int, k)
graph := make([][]int, k)
ans := make([]int, 0, k)
for _, edge := range edges {
// 减去1,简化代码,还原时加1即可
x, y := edge[0]-1, edge[1]-1
inDeg[y]++
graph[x] = append(graph[x], y)
}
q := make([]int, 0)
// 入度为0的表示起点,加入队列
for i := 0; i < k; i++ {
if inDeg[i] == 0 {
q = append(q, i)
}
}
// cnt标识扫描过的节点数,若扫描的节点数过多(k为负数),表示出现环
cnt := k
// 拓扑排序
for len(q) != 0 {
top := q[0]
q = q[1:]
cnt--
// 入结果队列
ans = append(ans, top)
// 所有下一跳节点入度减1
for _, next := range graph[top] {
if inDeg[next]--; inDeg[next] == 0 {
q = append(q, next)
}
}
}
if cnt != 0 {
return nil
}
return ans
}
func buildMatrix(k int, rowConditions [][]int, colConditions [][]int) [][]int {
row := topoSort(rowConditions, k)
col := topoSort(colConditions, k)
if row == nil || col == nil {
return nil
}
ans := make([][]int, k)
// 指定数字的row下标
rowIdx := make([]int, k)
for i, v := range row {
rowIdx[v] = i
}
// 指定数字的col下标
for j, v := range col {
ans[rowIdx[v]] = make([]int, k)
// 填入数字
ans[rowIdx[v]][j] = v + 1
}
return ans
}
最后修改于 2022-08-29